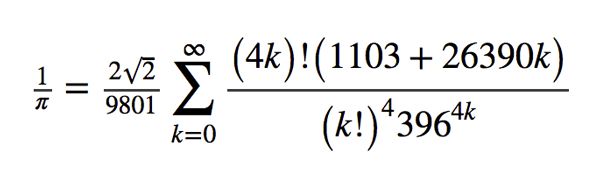National Geographic India - #DidYouKnow that one of these infinite series was used to calculate pi to more than 17 million digits? This #NationalMathematicsDay, let's celebrate one of the world's greatest mathematicians,
How accurate is Ramanujan's PI series? - Quora
0027: Part 6, Ramanujan's pi formulas and the hypergeometric function - A Collection of Algebraic Identities
Cliff Pickover on Twitter: "Mathematics. A formula from Indian mathematician Ramanujan. Golden Ratio, e, and Pi dance in delight. https://t.co/PWnPd0a3aW" / Twitter
Ramanujan: The Patron Saint of Pi Explorers – Bhāvanā
𝐒𝐫𝐢𝐧𝐢𝐯𝐚𝐬𝐚 𝐑𝐚𝐠𝐡𝐚𝐯𝐚 ζ(1/2 + i σₙ )=0 on Twitter: "In the year 1914, Srinivasa Ramanujan published a paper titled 'Modular Equations & Approximations to Pi' in Cambridge journal. In that Ramanujan gave
Ramanujan, the Man who Saw the Number Pi in Dreams | OpenMind
Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
Extra-math - 📊Ramanujan Pi-Formula & Derivation | Facebook
Convergent hypergeometric Ramanujan-like series for 1/π 2 | Download Table
Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
Pi Table with Ramanujans,Chudnovsky Formulas
Ramanujan's Magnificent Formula for Pi: 9801/(1103√8)=π | by Sunny Labh | Cantor's Paradise
Ramanujan-like formulae for $$\pi $$ and $$1/\pi $$ via Gould–Hsu inverse series relations | SpringerLink
National Mathematics Day 20212: 9 Interesting Facts about Genius Mathematician Srinivasa Ramanujan
Solved Ramanujan's Formula for Pi First found by Ramanujan. | Chegg.com
Ramanujan, the Man who Saw the Number Pi in Dreams | OpenMind
Joseph T Noony on Twitter: "Ramanujan's formula and its variants are today used by supercomputer algorithms for calculating pi correct to millions of decimals of accuracy! What a true genius he was
Solved Ramanujan's Formula for Pi First found by Ramanujan. | Chegg.com
New Proof Settles How to Approximate Numbers Like Pi | Quanta Magazine
Solved Ramanujan's sum of 1/pi The goal of this project is | Chegg.com
Ramanujan–Sato series - Wikipedia
Solved Around 1910, the Indian mathematician Srinivasa | Chegg.com
Best algorithm to calculate Pi - Part1
A monstrous formula : Ramanujan's approximation of pi
